【意外!!】エレキベースの周波数解析
Contents
はじめに
こんにちは。Tepoです。
初回である今回は、ベースの音にはどんな周波数が含まれているのかについて実験をしてみたいと思います。
問題です。ベースの3弦開放(ラの音)の周波数は何Hzでしょうか?
ググるとすぐわかりますが、55Hzです。
ただ、これは本当なのでしょうか?
試しに、実際の55Hzの音を聴いてみましょう。
音程は確かに合っていますが、3弦の音とは全く異なります。
どうやら、3弦開放弦の音には55Hzだけではなく、他の周波数も含まれているようです。
今回は、ベースにはどんな周波数が実際に含まれているのかについて実験をしてみたいと思います。
そもそも周波数って何?
周波数とは読んで字のごとく「周期的な波の数」略して「周波数」です。(「中二病」=「中学校二年生の男子みたいな病的な状態」と同じ理論です。)
周波数ではヘルツ(Hz)という単位が用いられます。Hzとは一秒間に何回空気が振動するかという意味です。
440Hzという数字を見たことがある方も多いかと思いますが、これは、一秒間に空気が440回振動するという意味です。
下の図1、図2は440Hzとその半分の220Hzをグラフにしたもの、そして音1、音2はその周波数で空気を振動させたもの(空気を振動させたもの、それすなわち音です!)となります。
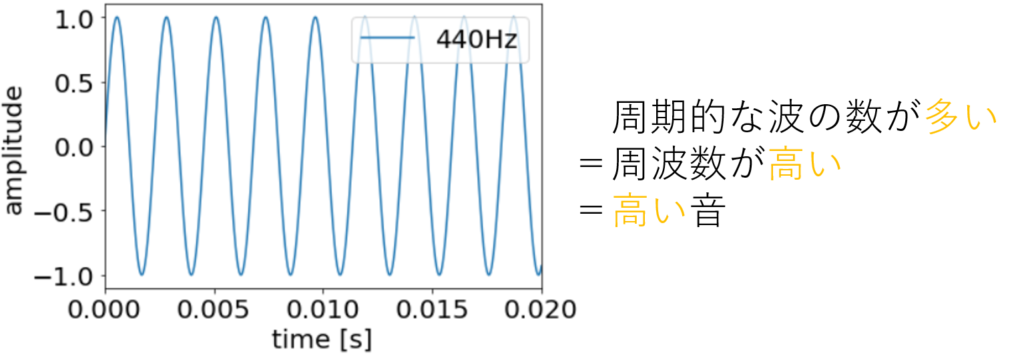
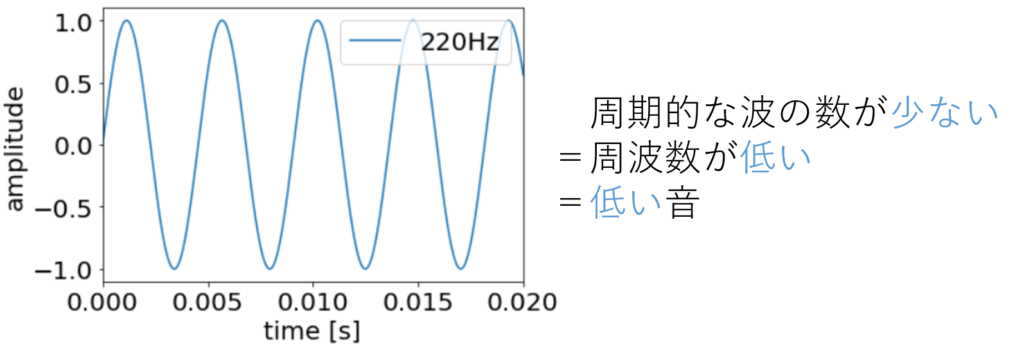
いかがでしょうか。周波数が空気の振動数であること、そしてその振動数が多いほうが高い音が出て、振動数が少ないほうが低い音が出るということがご理解いただけましたでしょうか?
周波数解析方法
では、どのようにして周波数を分析できるのでしょうか?
音声信号は時々刻々と変化しますので、含まれる周波数も時々刻々と変化します。
時間で変動する周波数を求める方法の一つとして、定Q変換(CQT)という手法を用います。
※当初STFT(短時間フーリエ変換)にて周波数解析を行っておりましたが、CQTに変更しました(10/20)
要望があれば解説をしたいと思いますが、スペクトログラムという横軸が時間縦軸が周波数そしてグラフエリアには濃淡で含まれる周波数の強弱を表したものを作成します。
音声信号を録音し、これにCQTをかけることで、含まれる周波数を求めてみます。
なお、本解析ではPythonでlibrosaという音声解析ライブラリを用いております。
librosaのCQTでは解析最低周波数を設定する必要がありますが、デフォルト値(32.70[Hz])にて行います。
今回は、指弾きで3弦開放の音を録音し、周波数解析をすることで、どんな周波数が含まれているのかを調べてみたいと思います。
ベースの音を周波数解析してみた
今回使用した機材は下記のとおりです
- ベース:Amaze ASM 4弦 (ESP)
- 弦:Red Strings (Nickel)(Warwick)
- ピック:PR1-BKH(SolidBond)
- SWITCHCRAFT 11(SWITCHCRAFT)
- シールド:LC01-SA BLACK(CANARE)
- オーディオインターフェース:UR22mkII(STEINBERG)
まずは、3弦開放の音をwav形式で録音します。
そして、このファイルを短時間フーリエ変換し、スペクトログラムを求めてみます。
なお、短時間フーリエ変換プログラムはPythonで作成しました。
需要があればこのプログラムや構築環境もブログに書きたいと思います。
解析した結果が下記の図3となります。
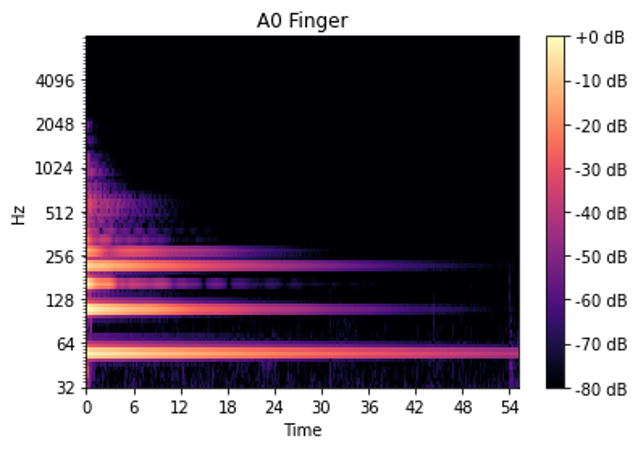
この図の見方は横軸が時間、縦軸が周波数そして描かれている色がある時刻における特定の周波数の強さを表しています。
カラースケールの通り、黄色に近いほどその周波数を多く含んでおり黒に近いほどその周波数を含んでいないことを示します。
図3より、基本周波数である55Hzが強く出ています。
また、110Hz、220Hzの倍音が多く含まれています。
55Hzの場合、2倍の110Hzおよび4倍の220Hzはオクターブ違いとなりますが、3倍(165Hz)の音は全く異なる音となります。
周波数解析の結果、3弦開放には基本周波数以外にも多くの周波数が含まれていることがわかりました。
考察(波という立場から考えてみる)
では、なぜこのような結果になったのかをベースという物体の構造から考えてみましょう。
ベースはブリッジとナットという両端で弦ががっちりホールドされています。
そしてこのホールドされた両端が支点となって、弦が振動しています。
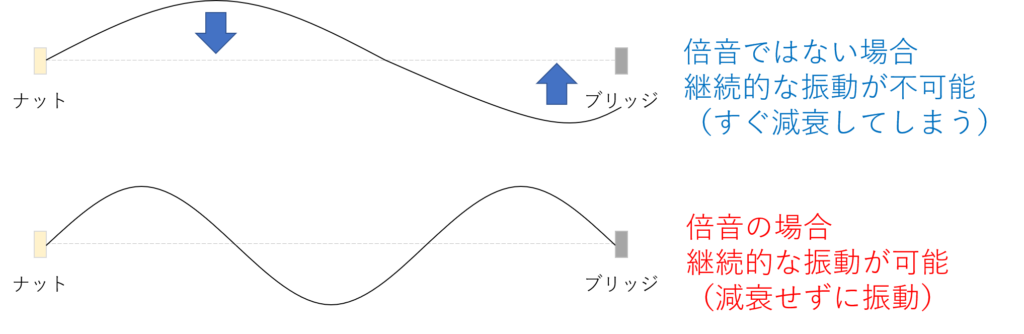
このような条件下において、弦が安定的に振動を継続できる周波数(波長)はいったいどのような状態でしょうか?
それは、図4のように、状態です。
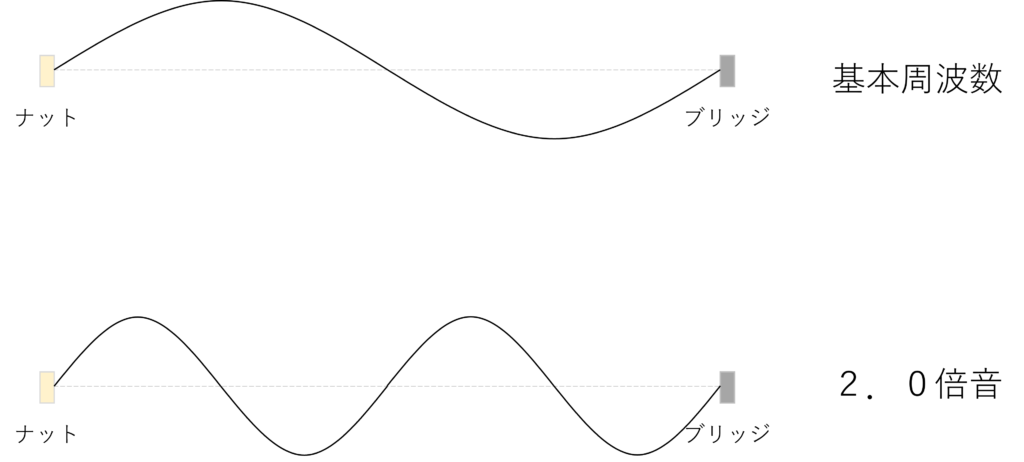
そう、まさしくそれは基本周波数の倍音であり、先ほどのスペクトログラムの正体です。
なお、基本周波数の倍音ではない中途半端な周波数はどうなるのかというと、図5のように安定的に存在することができず、即座に収束してしまいます。
検証(得られた波形をもとに疑似的に波形生成)
最後に、もう一つ検証をしてみましょう。
3弦開放には基本周波数に加えて複数の倍音周波数が含まれていることが分かったので、今度は逆に、複数の周波数をうまくブレンドすれば疑似的に3弦開放の音を再現できるのでは?と考えられます。
そこで、先ほどのスペクトログラムをもとに、各倍音をブレンドして「疑似3弦開放」をを作ってみました。
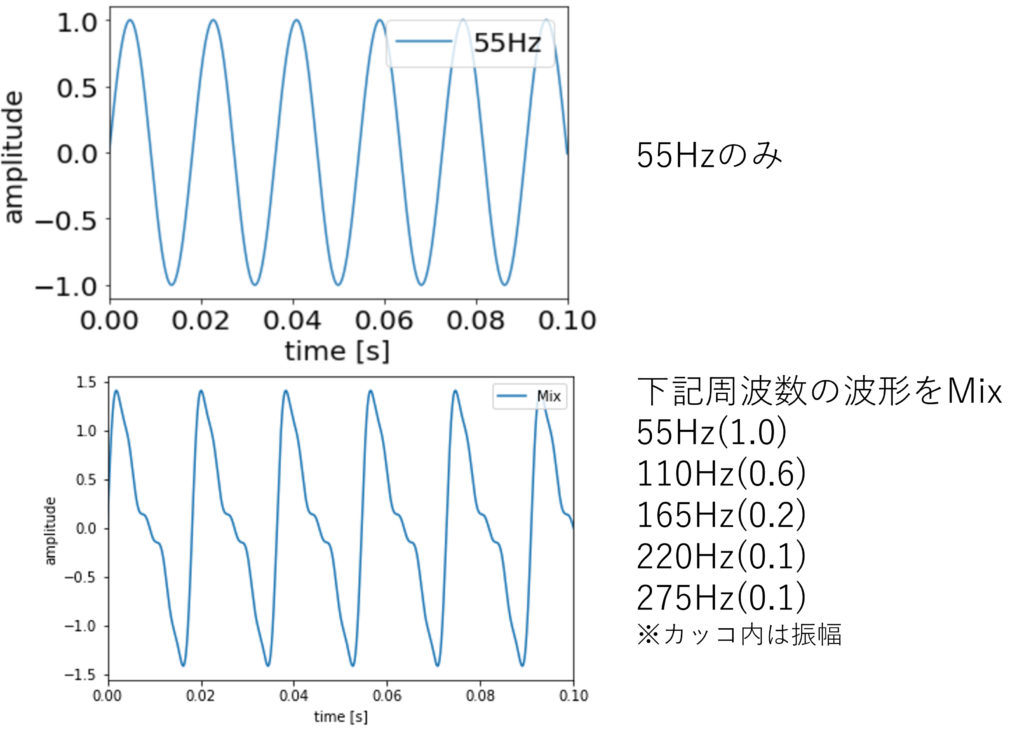
図6の波形を見ると、55Hz単一周波数の波形よりもいい感じに複雑になっています。
音を聴き比べるといかがでしょうか?
疑似的に生成した音声ファイルの方がいい意味で荒々しく、実際の3弦開放の音に近いのではないかと私は思います。
ただ、やはりまだ実際の音とは違うのは明確です。
これは、実際の音はさらに多くの倍音を含んでいること、また各周波数によって振動が減衰するタイミング等が異なること等、様々な要因が挙げられます。
シンセサイザーはまさにこれをいじくって音を作り出す楽器です。複数の波形を操って一つの音を作り出すのはまさに職人技ですよね!
まとめ
今回は3弦開放の音に含まれる周波数を周波数分析し、どのような周波数が含まれているのかを実験しました。
日頃何気なく「倍音が効いてるんだよ」と言っていても実際の倍音の周波数や波形を見るとより具体的なイメージとして捉えられ、音づくり等にもいい影響があるのかなと思います。
スペクトログラムを用いた周波数解析でまだまだ色々な実験ができそうなので、順次ブログ化します。
是非ご一読いただけますと幸いです。






ディスカッション
コメント一覧
まだ、コメントがありません